• 迪菲-赫尔曼密钥交换
• Signal 宣称加密传输，既服务器是无法解密用户的消息，只有对方能解密，其中用到的就是迪菲-赫尔曼密钥交换
• 假设两个用户 用户1 和 用户2
• 首先他们协商两个公开数据：p = 23, g = 5 这个是公开的
• 用户1定义一个私密数字 a = 6， 计算 A = g^a % p，A 可以当一个公钥发送给用户2
• 用户2定义一个私密数字 b = 15，计算 B = g^b % p，B 也是当作一个公钥发送给用户1
• 用户1收到公钥 B 后，再计算 s = B^a % p
• 用户2收到公钥 A 后，再计算 s = A^b % p
• 这个时候你会神奇发现他们算出来的值相等，都是2
• 然后用这个值对消息进行对称加密
• 也就是说

p = 23,g = 5 // 常数
(g^b % p)^a % p = (g^a % p)^b % p

• 怎么证明这玩意相等呢
• 根据二项式定理
• 
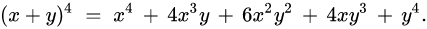
• (xp + y)^4 = (xp)4 + 4(xp)^3y + 6(xp)^3*y^2 + 4(xp)y^3 + y^4
• 已知 m = np+l 那么 m % p = l
• 那 (xp + y)^4 % p = 0 + 0 + 0 + 0 + y^4 % p = y^4 % p
• 令 g = xp + y
• g^b = (xp+y)^b = nC0(y)^b + nC1(xp)y^(b - 1)+ …+nCn(xp)^b
• g^b % p = (xp+y)^b % p = y^b % p
• 然后再令 y^b = kp + j 那 y^b % p =（kp + j) % p = j
• 所以 (g^b % p)^a % p = (y^b % p)^a % p = j^a % p
• 然后再算一下 g^(ab) % p = (xp + y)^(ab) % p = y^ab % p = (y^b)^a % p = (kp+j)^a % p = j^a % p
• 所以 (g^b % p)^a % p = g^(ab) % p = (g^a % p)^b % p